Shadowing lemma

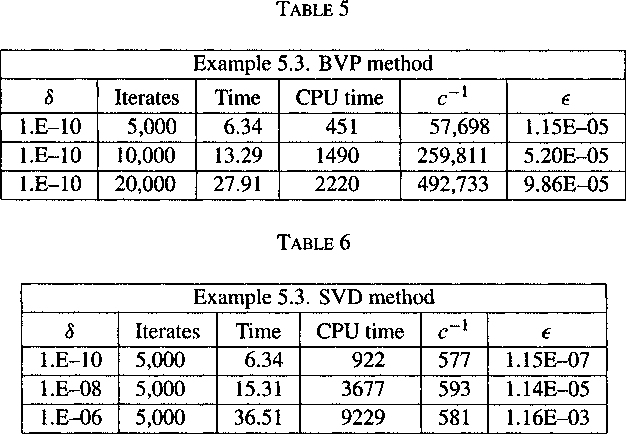
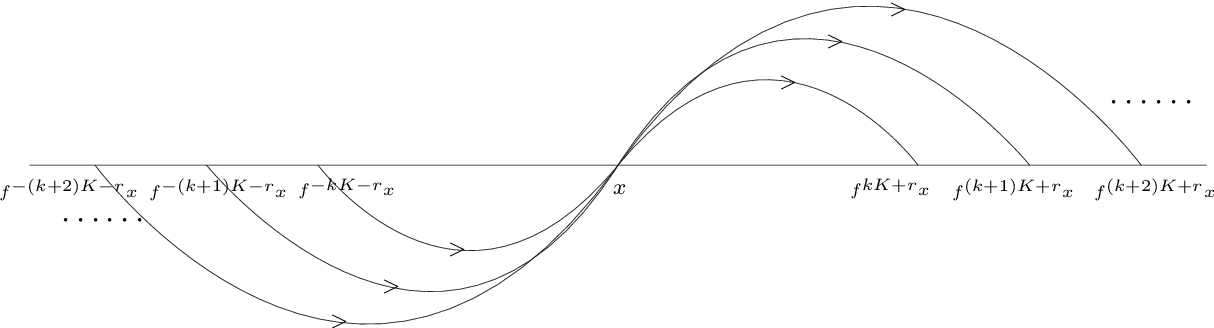
In the theory of dynamical systems, the shadowing lemma is a lemma describing the behaviour of pseudo-orbits near a hyperbolic invariant set. Informally, the theory states that every pseudo-orbit (which one can think of as a numerically computed trajectory with rounding errors on every step) stays uniformly close to some true trajectory (with slightly altered initial position)—in other words, a pseudo-trajectory is "shadowed" by a true one. This suggests that numerical solutions can be trusted to represent the orbits of the dynamical system. However, caution should be exercised as some shadowing trajectories may not always be physically realizable.

Formal statement

Given a map f : X → X of a metric space (X, d) to itself, define a ε-pseudo-orbit (or ε-orbit) as a sequence ${\displaystyle (x_{n})}$ of points such that ${\displaystyle x_{n 1}}$ belongs to a ε-neighborhood of ${\displaystyle f(x_{n})}$.

Then, near a hyperbolic invariant set, the following statement holds: Let Λ be a hyperbolic invariant set of a diffeomorphism f. There exists a neighborhood U of Λ with the following property: for any δ > 0 there exists ε > 0, such that any (finite or infinite) ε-pseudo-orbit that stays in U also stays in a δ-neighborhood of some true orbit.

${\displaystyle \forall (x_{n}),\,x_{n}\in U,\,d(x_{n 1},f(x_{n}))<\varepsilon \quad \exists (y_{n}),\,\,y_{n 1}=f(y_{n}),\quad {\text{such that}}\,\,\forall n\,\,x_{n}\in U_{\delta }(y_{n}).}$

See also

• Chaotic systems
• Butterfly effect

References

External links

• Shadowing Theorem on Scholarpedia
• Can a butterfly in Brazil control the climate of Texas?